Numerical and analytical study of undular bores governed by the full water wave equations and bi-directional Whitham-Boussinesq equations
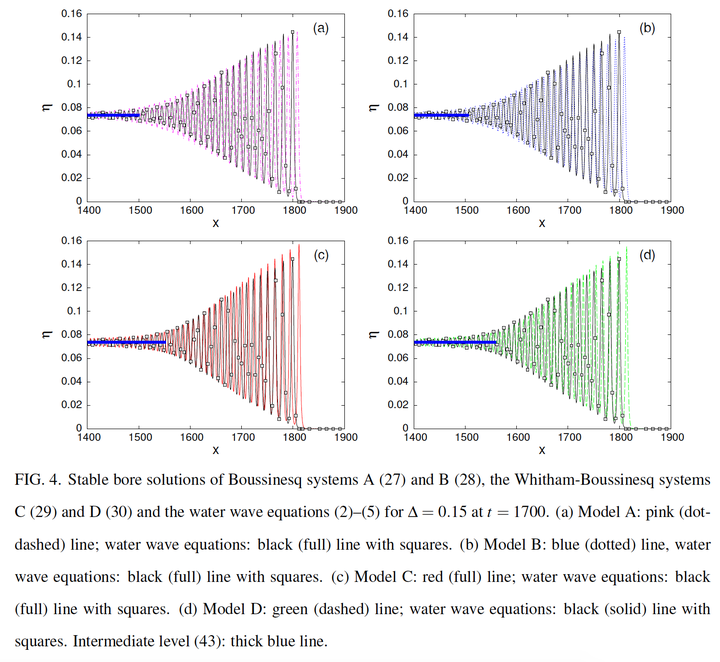 Image credit: Unsplash
Image credit: Unsplash
Abstract
Undular bores, also termed dispersive shock waves, generated by an initial discontinuity in height as governed by two forms of the Boussinesq system of weakly nonlinear shallow water wave theory, the standard formulation and a Hamiltonian formulation, two related Whitham-Boussinesq equations and the full water wave equations for gravity surface waves are studied and compared. It is found that the Whitham-Boussinesq systems give solutions in excellent agreement with numerical solutions of the full water wave equations for the positions of the leading and trailing edges of the bore up until the onset on modulational instability.The Whitham-Boussinesq systems, which are far simpler than the full water wave equations, can then be used to accurately model surface water wave undular bores. Finally, the Whitham-Boussinesq systems give slightly lower borderlines in the initial jump height for the onset of modulational instability.
Supplementary notes can be added here, including code and math.