Linear Modes for Channels of Constant Cross- Section and Approximate DirichletNeumann Operators

Abstract

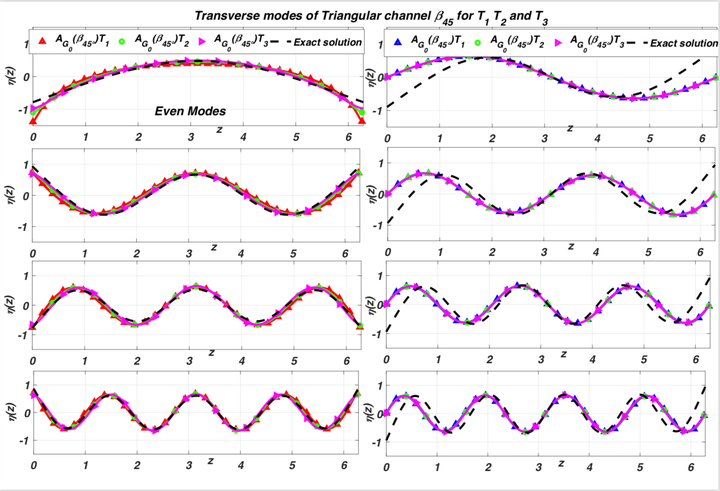
We study normal modes for the linear water wave problem in infinite straight channels of bounded constant cross-section. Our goal is to compare semi-analytic normal mode solutions known in the literature for special triangular cross-sections to numerical solutions obtained using approximations of the non-local Dirichlet–Neumann operator for linear waves, specifically an ad-hoc approximation proposed in Vargas-Magaña and Panayotaros, and a first-order truncation of the systematic depth expansion by Craig et al. We consider cases of transverse (i.e. 2-D) modes and longitudinal modes, i.e. 3-D modes with sinusoidal dependence in the longitudinal direction. The triangular geometries considered have slopping beach boundaries that should in principle limit the applicability of the approximate Dirichlet–Neumann operators. We nevertheless see that the approximate operators give remarkably close results for transverse even modes, while for odd transverse modes we have some discrepancies near the boundary. In the case of longitudinal modes, where the theory only yields even modes, the different approximate operators show more discrepancies for the first two longitudinal modes and better agreement for higher modes. The ad-hoc approximation is generally closer to exact modes away from the boundary.